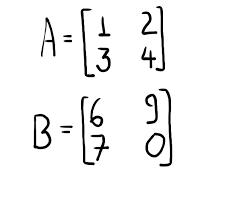تعریف ماتریس در متلب
ماتریسها بهعنوان نمایش اساسی از اطلاعات و داده در محیط نرمافزار Matlab شناخته میشوند. درواقع، ماتریس نوعی آرایه دو بعدی است که زیرمجموعهای از آرایه محسوب میشود و از قوانین جبر خطی پیروی میکند. ماتریسها به لحاظ ساختاری بهشکل سطرها و ستونهای مختلف تعریف میشوند.
تعداد ستونها برای یک ماتریس بسته به میزان و نوع داده میتواند از یک تا n باشد؛ همچنین تعداد سطرهای آن، نیز از یک ردیف وجود دارد و امکان تشکیل m ردیف وجوددارد. اگر تعداد سطرها و ستونهای یک ماتریس با همدیگر برابر باشند، به آن ماتریس مربعی گفته میشود. عملگرهای زیادی برای ماتریسها وجود دارند که میتوان برروی آنها تغییراتی اعمال کرد.
برخی از این عمگرها مانند جمع و تفریق عملگرهای جبری هستند. برخی دیگر از تغییرات شامل تعاریف جدیدی چون دترمینان، ترانهاده و معکوس ماتریس میشوند. معکوس ماتریس، یکی از دستورات کاربردی در مطلب است که قصد داریم درادامه به آن بپردازیم. نرمافزار متلب یکی از بهترین محیطهای برنامهنویسی برای استفاده از ماتریسها محسوبمیشود.
برای ساختن یک ماتریس در متلب، کافیست تک تک عناصر را تعریفکنید. درهمین راستا، برای مشخصنمودن چندین عنصر در یک ردیف یا سطر، عناصر را با علامت ویرگول یا فاصله از هم جدا کنید. همچنین قراردادن علامت نقطهویرگول، به شما کمک میکند تا سطرها از یکدیگر متمایز شوند و فاصله بین هر نقطهویرگول یک ستون تعریف شود.
معکوس ماتریس در متلب چیست
معکوس ماتریس در متلب، یکی از دستورات کاربردی ماتریسها بهشمار میرود که میتوان به آن اشاره کرد. معکوسکردن ماتریس، دراصل عملیاتی است که برای ضرب و تقسیم ماتریسها بهکار میرود؛ زیرا ماتریسها در عملیات ضرب و تقسیم مانند اعداد معمولی عمل نمیکنند. برای این کار از مفهوم معکوس ماتریس استفاده میشود.
ماتریسها کاربرد گستردهای در علوم کامپیوتر و داده، مهندسی، فیزیک، الکترونیک، ریاضیات و غیره دارد. بهعنوان مثال، برای تعریف بردارهای سرعت، تانسورهای شتاب، فشار، تنش و سایر کمیتهای چند بعدی میتوان از ماتریس استفاده کرد. معکوس کردن ماتریسها در حل معادلات خطی، بسیار رایج و خوب است.
عملگرهایی مانند معکوس ماتریس با قوانین جبری اعداد کمی متفاوتاند. بسیاری از افراد به اشتباه تصور میکنند، معکوس ماتریس به معنای معکوس کردن هر یک از اعداد آن است، اما اینگونه نیست! برای اینکه بتوان معکوس یک ماتریس را بدست آورد، ماتریس باید یکسری قوانین و شرایط خاصی داشتهباشد. بنابراین ممکناست معکوس یک ماتریس همیشه وجود نداشتهباشد.
برای محاسبه معکوس ماتریس، روشهای ریاضی متعددی وجود دارد، اما این کار بسیار زمانبر است؛ چون دادههایی با حجم بالا شامل اعداد مختلف و بسیاری هستند، درنتیجه ممکن است خطای محاسبات وجود داشته باشد یا حتی امکان محاسبه این همه اطلاعات وجود نداشتهباشد. درچنین مواقعی از دستور معکوس ماتریس در محیط متلب استفاده میکنیم.
دستور معکوس ماتریس در متلب
در بخش قبلی گفتیم، محاسبه معکوس ماتریس به روش دستی همیشه امکانپذیر نیست؛ همچنین محاسبات ازطریق ماشینحساب هم محدودیت دارد و ماتریسهایی با سطر و ستونهای زیاد، قابل انجام نیستند. در اینقسمت به نحوه استفاده از این دستور در Matlab میپردازیم. ابتدا برای تشکیل ماتریس باید به دو نکته مهم توجهکنید:
ماتریس باید مربع باشد؛ یعنی اگر بخواهید معکوس ماتریس را بدست آورید، باید تعداد سطرها و ستونهای تعریفشده یکی باشد.
اگر دترمینان یک ماتریس صفر باشد، معکوس وجود ندارد و ماتریس مفرد است.
دترمینان یک ماتریس مربع، یک کمیت اسکالر است که در ادامه عملیات معکوسکردن، لازم است. یافتن دترمینان ماتریسهای ۲×۲ و ۳×۳ نسبتا آسان است و مطابق شکل زیر محاسبه میشود، اما ماتریسهای مرتبه بالاتر پیچیدگی خود را دارد. اگر دترمینان ماتریس صفر باشد، خروجی دستور، خطا خواهدبود.

یکی از راههای تشکیل ماتریس بهعنوان داده ورودی، تعریف خود ماتریس است. درهمین راستا، کافی است یک فایل اسکریپت (script file) جدید ایجاد نمایید. در این بخش، برای ماتریس یک نام یا مشخصه مانند a تعریف میکنید. سپس بهترتیب شکل زیر، دادههای خود را وارد میکنید. در خط بعدی، نوشتن تابع inv(a) معکوس ماتریس تعریفشده را به شما خواهد داد. اگر تعداد آرگومان ورودی زیاد و به صورت دامنهای از اعداد باشد، میتوان با تعریف ماتریس a بهصورت یک بازه، آن را تشکیل داد.
درواقع معکوس یک ماتریس A، درحالت کلی با A-1 نشان داده می شود به طوری که رابطه AA−۱ = A−1A = 1 برقرار است. نکتهای که وجود دارد، عکس یک ماتریس، یک ماتریس جدید با همان مرتبه است. دستور معکوس ماتریس در متلب با استفاده از تابع inv() تعریف شدهاست. بدینترتیب یک ماتریس مانند A را درنظر بگیرید، معکوس آن با تعریف تابع inv(A) بهدست میآید.