تردیدی نیست که انتگرال، پایه و بنیاد مهندسی است و نقش مهمی را در محاسبات اساسی ریاضی و مهندسی ایفا میکند. از طرفی محاسبه انتگرال همیشه هم چندان ساده و بیمشکل نیست و محاسبه دستی آن، ممکن است زمان زیادی از ما بگیرد؛ به همین دلیل بسیاری از افراد دنبال روشی مطمئن و ساده برای محاسبه انتگرال میگردند. یکی از بهترین روشهای انتگرالگیری، کمک گرفتن از نرم افزار متلب است. در این مقاله تصمیم داریم به آموزش انتگرال گیری در متلب بپردازیم و راه و روش این کار را به صورت کامل و ساده توضیح دهیم.
در صورتی که شما هم تمایل دارید شیوه محاسبه انواع انتگرال در زبان متلب را یاد بگیرید، کافی است چند دقیقه زمان بگذارید و تا انتهای این مقاله با ما همراه شوید.
دستهبندی انتگرالها؛ نکتهای مهم قبل از آموزش انتگرال گیری در متلب
دنیای انتگرالها را میتوانیم به دو نیمکره تقسیم کنیم که نیمکره اول به انتگرال معین و نیمکره دیگر به انتگرال نامعین تعلق دارد. انتگرال معین به انتگرالی گفته میشود که در آن، بازه انتگرالگیری مشخص است. در این نوع از انتگرال، دنبال یافتن مقدار تابع در بازه مشخصشده هستیم. مثلاً انتگرال تابع x۲ در بازه ۰ تا ۱، برابر با یکسوم است. در واقع برای محاسبه انتگرال معین در متلب، باید بازه انتگرالگیری را به صورت کامل مشخص کنیم.
انتگرال نامعین، انتگرالی است که در آن بازه انتگرالگیری مشخص نیست. هدف از انتگرالگیری نامعین، یافتن تابعی است که مشتق آن، همان تابعی است که داریم انتگرالش را میگیریم. به عنوان مثال انتگرال نامعین تابع 3x۲ برابر با x۳ است. خوشبختانه امکان انتگرال گیری نامعین در متلب نیز وجود دارد.
انتگرال گیری نامعین در متلب
در حال حاضر امکان محاسبه هر نوع مشتق و انتگرال در متلب وجود دارد. ما در این بخش از مقاله میخواهیم شیوه محاسبه انتگرال نامعین در متلب را توضیح دهیم. برای محاسبه انتگرال تابع f(x) از دستور زیر استفاده میکنیم:
int(f);
فرض کنید میخواهیم انتگرال تابع 2x را محاسبه محاسبه کنیم. برای این کار، برنامه زیر را مینویسیم. توجه داشته باشید که برای تعریف متغیرها در متلب از دستور syms کمک میگیریم.
syms x
int(2*x)
وقتی کدهایی که نوشتهایم را اجرا کنیم، متلب نتیجه انتگرالگیری را به شکل زیر به ما میدهد:
ans =
x^2
یک مثال دیگر برای انتگرال گیری در متلب از نوع نامعین
در مثال زیر میخواهیم انتگرال برخی از عبارات متداول را محاسبه کنیم. برای این کار کد زیر را مینویسیم:
syms x n
int(sym(x^n))
f = ‘sin(n*t)’
int(sym(f))
syms a t
int(a*cos(pi*t))
int(a^x)
در صورت اجرای این برنامه، متلب، نتیجه زیر را به ما میدهد:
ans =
piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)])
f =
sin(n*t)
ans =
-cos(n*t)/n
ans =
(a*sin(pi*t))/pi
ans =
a^x/log(a)
محاسبه انتگرال معین در متلب
وقتی میخواهیم مساحت بین یک منحنی و محور x را محاسبه کنیم، ناچاریم از انتگرال معین کمک بگیریم. برای محاسبه انتگرال تابع f(x) از a تا b، از دستور زیر استفاده کنید:
int(x, a, b)
برای محاسبه تابع x از نقطه ۴ تا ۹، دستور زیر را مینویسیم:
int(x, 4, 9)
اگر این برنامه را اجرا کنیم، نتیجه زیر را میگیریم:
ans =
۶۵/۲
یک مثال برای محاسبه انتگرال معین در متلب
در این مثال میخواهیم انتگرال y= x۳-2x+5 را از x=1 تا x=2 را محاسبه کنیم. برای این کار باید کد زیر را بنویسیم:
f = x^3 – 2*x +5;
a = int(f, 1, 2)
disp(‘Area: ‘), disp(double(a));
پس از اجرای این برنامه، جواب زیر را میگیریم:
a =
۲۳/۴
Area:
۵.۷۵۰۰
محاسبه انتگرال دوگانه در متلب
برای محاسبه انتگرال دوگانه در متلب باید از دستور int کمک بگیریم. فرض کنید که میخواهیم انتگرال زیر را محاسبه کنیم:
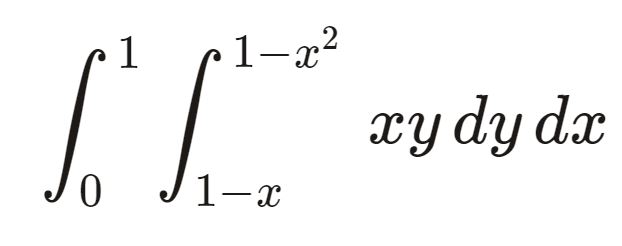
برای محاسبه این انتگرال باید کد زیر را بنویسیم و اجرا کنیم:
syms x y
firstint=int(x*y,y,1-x,1-x^2)
answer=int(firstint,x,0,1)
اگر با این مدل کدنویسی راحت نیستید، میتوانید از کد زیر استفاده کنید:
int(int(x*y,y,1-x,1-x^2),x,0,1)
با اجرا کردن این دو دستور، پاسخ ۱/۲۴ را از متلب دریافت میکنید.
دستور integral2؛ راهکاری دیگری برای محاسبه انتگرال دوگانه در متلب
روشی دیگر به نام «integral2» برای محاسبه انتگرالهای دوگانه در متلب وجود دارد که میتواند کار را برای کاربران راحت کند. در این روش منظور از fun، همان تابع و منظور از xmin، xmax، ymin و ymax، کرانهای دو متغیر هستند. توجه داشته باشید که در این روش، باید عملگرها را با «.» وارد کنید. به عنوان مثال در هنگام وارد کردن عملگرد ضرب، نباید فقط «*» را وارد کنید؛ بلکه باید این عملگر را به شکل «.*» وارد کنید. همچنین برای تعریف متغیرها از نشانه «@» کمک بگیرید. به مثال زیر دقت کنید تا موضوع را به صورت کامل دریابید.

فرض کنید میخواهید انتگرال تابع زیر را «در بازه ۰ تا عدد پی» برای x و y محاسبه کنیم.
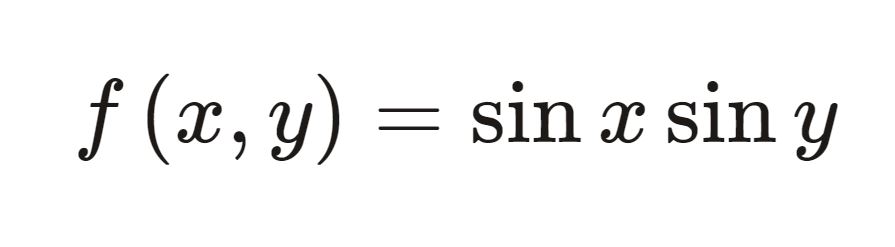
برای محاسبه انتگرال تابع فوق در بازه مورد نظر، باید کد زیر را بنویسیم:
z=@(x,y) sin(x).*sin(y);
integral2(z,0,pi,0,pi)
با اجرای دستور فوق، متلب پاسخ ۴ را برای شما نمایش میدهد.
روش محاسبه انتگرال عددی در متلب
برای محاسبه انتگرال عددی در متلب، روشهای مختلفی وجود دارد که ما در این مقاله تنها دو روش سیمپسون و ذوزنقهای را آموزش میدهیم.
۱. روش سیمپسون برای حل انتگرال در متلب
وقتی میخواهیم به روش سیمپسون، انتگرالگیری کنیم، باید بدانیم که این روش به دو فرم، سیمپسون ۱/۳ و سیمپسون ۳/۸ صورت میگیرد. برای محاسبه انتگرال عددی به شیوه سیمپسون باید از دستور simpsons(f,a,b,n) کمک بگیرید. منظور از f، همان تابع است، a و b نقاط ابتدایی و انتهایی بازه هستند و n، تعداد زیربازههاست.
فرض کنید که میخواهیم انتگرال عدد تابع f(x)=x.Sin(x) را در بازه [۱,۰] با ۴ زیربازه محاسبه کنیم. برای این کار از کد زیر کمک میگیریم:
function [integral] = simpson(f, a, b, n)
h = (b – a) / n;
integral = 0;
for i = 1:n
x = a + (i – 1) * h;
if i == 1 || i == n
integral = integral + f(x);
else
integral = integral + 4 * f(x);
end
end
integral = integral * h / 3;
return integral;
f = @(x) x * sin(x);
a = 0;
b = 1;
n = 4;
integral = simpson(f, a, b, n);
disp(integral)
پس از اجرای این کد، متلب، نتیجه زیر را به شما نمایش میدهد:
۰.۷۶۰۱۲۷۷۹۰۰۵۵۵۶۶۵
۲. روش ذوزنقهای با دستور trapz در متلب
روش ذوزنقهای، روش دیگری برای محاسبه انتگرال عددی در متلب است. فرض کنید میخواهیم با انتگرال عددی به روش ذوزنقهای، انتگرال f(x)=Sin(x) را در بازه [۰, π] محاسبه کنیم. برای این کار باید کد زیر را در متلب بنویسیم:
function [integral] = trapezoidal(f, a, b, n)
h = (b – a) / n;
integral = 0;
for i = 1:n
x = a + (i – 1) * h;
integral = integral + (f(x) + f(a)) / 2 * h;
end
return integral;
f = @(x) sin(x);
a = pi;
b = 0;
n = 4;
integral = trapezoidal(f, a, b, n);
disp(integral)
پس از اجرای این دستور، نتیجه زیر نمایش داده میشود:
۱.۹۹۶۰۶۴۷۹۸۳۹۴۸۲۷۹
آموزش مقدماتی تا پیشرفته متلب با دورههای آموزشی پلتفرم مکتبخونه
در این مقاله تلاش کردیم به آموزش انتگرال گیری در متلب بپردازیم و روشهای مختلف حل انتگرال در متلب را بیان کنیم. امیدواریم نکات و آموزههای این مقاله به شما کمک کند که کلیه انتگرالهای مورد نظر خود را بدون مشکل و دستانداز، حل کنید.

در صورتی که تمایل دارید برنامهنویسی در متلب را یاد بگیرید و مسائل مختلف ریاضی را در این نرم افزار حل کنید، پیشنهاد میشود که در دورههای آموزشی حرفهای و تخصصی شرکت کنید. مکتبخونه، یکی از پلتفرمهای آموزشی است که دورههای آموزشی مختلفی برای یادگیری کار با نرمافزار متلب در وبسایت خود عرضه کرده است. در صورت تمایل به کسب اطلاعات بیشتر در مورد این دورهها و شرکت در آنها، کافی است به صفحه آموزش متلب مراجعه کنید.
از نظر شما برای انتگرال گیری از ماتریس در متلب، باید از چه روشی استفاده کرد؟ برای محاسبه انتگرال بی نهایت در متلب باید از چه دستوری استفاده کرد؟ از دیدگاه شما، چه نرم افزار دیگری غیر از متلب، برای محاسبه انتگرال مناسب است؟ لطفاً نظرها، تجربیات و پیشنهادهای خود را با ما و سایر همراهان مکتبخونه در بخش دیدگاهها (زیر همین مقاله) به اشتراک بگذارید.