برنامه ریزی خطی چیست
برنامه ریزی خطی به زبان ساده
مقدمه
با پیشرفت تکنولوژی و گسترش سازمانها، تصمیمگیری کمی دشوار شدهاست. برای اینکه بتوانید تولید خودتان را به جلو ببرید و بیشترین سود ممکن نصیب شما شود، باید برنامه ریزی خطی کنید. برنامهریزی نیاز به نیروی انسانی خبره و هزینه و همچنین زمان دارد.
چگونه میتوان با کمترین نیروی انسانی ممکن و در کمترین زمان و همچنین با با حداقل هزینه به بیشترین سود رسید؟ برنامه ریزی باعث صرفه جویی در هزینه و همچنین وقت میشود. برنامه ریزی خطی (Linear Programming) روشی است که کمک می کند تا کمترین و بیشترین مقدار یک تابع خطی را بدست آوریم.
برنامه ریزی خطی، در علوم ریاضی، مدیریت، اقتصاد و … مورد استفاده قرار میگیرد. یعنی در علوم مهندسی، شهرسازی، مسائل اقتصادی، مسائل حکومتی و ارتش کاربرد گسترده ای دارد و به حل مسائل این ارگان ها کمک شایانی کرده است.

درکل این امکان را فراهم می کند تا با محدودیت های موجود بهترین تصمیم را بگیریم. برنامه ریزی خطی یا بهینه سازی خطی، یک روش ریاضیاتی است. این نوع برنامه ریزی، هنگام جنگ جهانی دوم شکل گرفت. زیرا در آن زمان نیاز داشتند تا هزینه ها را کاهش دهند و از طرفی هزینه های دشمن را بیشتر کنند.
این برنامه ریزی به حدی روش قابل اطمینانی است که حتی در حساس ترین لحظات هم می توان از آن استفاده کرد. همچنین تاثیرات شگرفی با خود به همراه داشته است و این امکان را فراهم آورده است، تا شرکت های مختلف در سراسر جهان تا میلیاردها دلار در هزینه ها صرفه جویی کنند.
به طور کلی مهمترین تاثیر مثبت برنامه ریزی خطی، کاهش هزینه ها است. به دلیل خطی و درجه اول بودن تمامی توابع و روابط در این برنامه ریزی، دلیل اصلی نامگذاری این نوع برنامه ریزی می باشد.
چند مثال برای درک بهتر برنامهریزی خطی:
مثال یک:
فرض کنید شما کارخانه ی رب سازی دارید و می خواهید رب ها را به انبارهایتان در شهرهای دیگر ارسال کنید. شما 10 کامیون دارید و می خواهید به 20 شهر رب ارسال کنید. چگونه میخواهید بهترین مسیر و زمان را انتخاب کنید و به راننده ها اطلاع بدهید؟
مثال دو:
اگر بخواهیم مساله را بازتر کنیم یک مثال دیگر به ما کمک میکند. فرض کنید شما یک تولیدی لباس دارید و تی شرت (T) و مانتو (M) تولید می کنید. تقاضای مانتو بیشتر است و هرچقدر شما مانتو تولید کنید مشتریها خرید می کنند. تی شرت هم در هر هفته حدود 50 متقاضی دارد.

برای تولید مانتو شما یک ساعت زمان لازم دارید و برای تولید تی شرت هم 2 ساعت زمان لازم دارید. در کل شما در هر هفته هم می توانید 400 ساعت را صرف تولید کنید. در هر هفته پارچه های لازم برای تولید 80 مانتو در دسترس است.
ولی پارچه های لازم برای تولید بیشتر تی شرت در دسترس است. سود ما به ازای تولید هر تی شرت 10000 تومان و به ازای تولید هر مانتو 7000 تومان است. برای اینکه سود بیشتر باشد باید چگونه برنامه ریزی کرد؟
سود= سود حاصل از تی شرت+ سود حاصل از مانتو
شما باید میزان سود را بیشتر کنید. از طرفی شما در تولید مواد اولیه محدودیت دارید. باتوجه به مواد اولیه، زمان، نیاز مشتری و محدودیت ها، معادله هایی به صورت زیر برقرار است.
T2+M1 ≤ 400 ساعت برای تولید لباس در هر هفته
تی شرت ≤ 50 (محدودیت تولید مانتو)
مانتو ≤ 80 (محدودیت در مواد اولیه)
اگر تولید مانتو را روی محور x و تولید شلوار را روی محور y رسم کنید، نموداری که ایجاد می شود بیشترین ظرفیت تولید در ترکیب های تی شرت و مانتو را نشان می دهد.

انتهای این نقاط روی محور x و y بیشترین تعداد مانتو و تی شرت هایی است که می توانید تولید کنید. در این مثال چهار نقطه ی x، y، w و z را فرض کنید. برای اینکه نقطه ی بهینه را بدست آود باید تمام این نقاط را بررسی کرد.
بیشترین سود در نقطهی w
T = ۰, M = 80
10000T+7۰۰۰M = حداکثر سود
560000=(7۰۰۰x80) + (100۰۰x۰) =سود
بیشترین سود در نقطهی z
T = ۱۰۰, M = ۰
100۰۰T+7۰۰۰M = حداکثر سود
1000000= (7۰۰۰x0)+(100۰۰x۱۰۰) = سود
بیشترین سود در نقطهی x
2T+1M=400
M = 80
مقدار M را در معادلهی اول عوض و برای T حل کنید:
2T+(5*80)
2T=400
200 =T
پس در این حالت، تولید عبارت است از 200 تی شرت و 80 مانتو،
10000T+7۰۰۰M = حداکثر سود
(7۰۰۰x80)+(100۰۰x20۰)=سود
56۰۰0۰+200۰۰۰۰= سود
2560000 = سود
بیشترین سود در نقطهی y
2T + 1M = 400
T = ۱۰۰
در معادلهی اول، مقدار T را ۱۰۰ در نظر بگیرید:
1M+(2*100)=400
1 M = ۲00
M=200
100۰۰T+7۰۰۰M = حداکثر سود
(7۰۰۰x200)+(100۰۰x۱۰۰) = سود
2400۰۰۰=100۰۰۰۰+1400۰۰۰ = سود
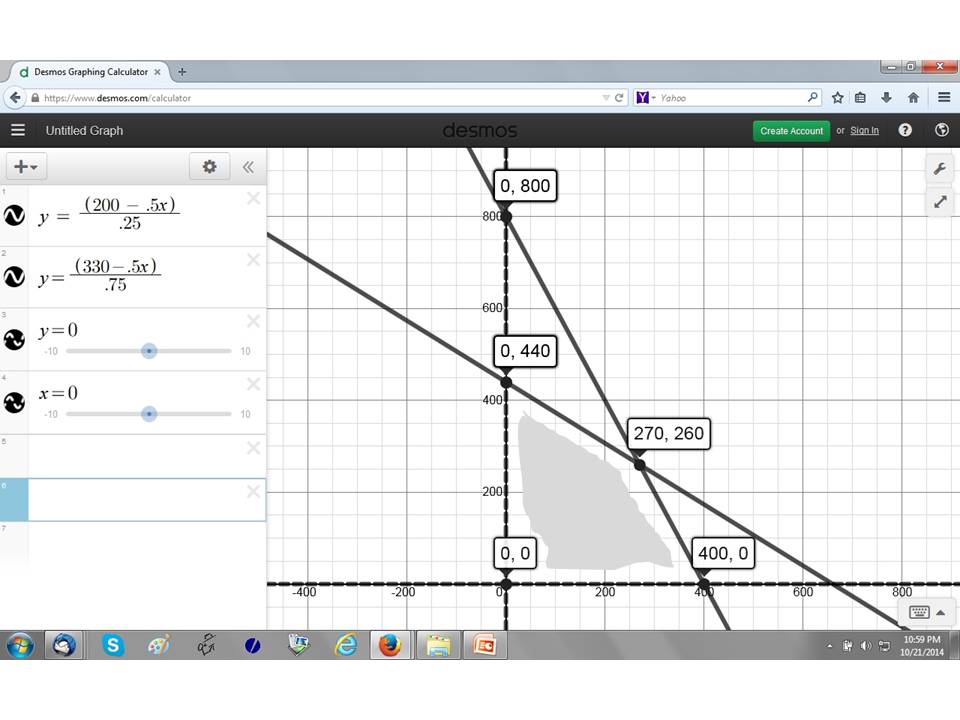
طبق محاسباتی که انجام شد، بیشترین سود در نقطه ی x است یعنی تولید 200 تی شرت و 80 مانتو بالاترین سود ممکن را به ما می دهد.
برنامه ریزی خطی به ما کمک تا با این سه خط معادله ای که داریم، ترکیب بهینه ای ایجاد کنیم. زیرا برنامه ریزی خطی در مرز بیرونی ترکیب بهینه ایجاد می کند. در مرز درونی امکان استفاده از همه ی معادله های ما برای ترکیب بهینه وجود ندارد. این ساده ترین مساله ای بود که بیان کردیم. معمولا پیچیدگی شرکت ها بیشتر از این چیزها است.
نحوهی محاسبهی برنامهریزی خطی:
نرمافزارهایی مانند متلب این امکان را فراهم میکنند تا بتوانیم از طریق آنها برنامهریزی خطی را پیادهسازی کنیم و مسائل پیچیده را حل کنیم و به جواب برسیم و بهترین ترکیب ممکن برای تولید تی شرت و مانتو و یا هر محصول دیگر را برای ما مشخص می کند.





