آموزش درون یابی در متلب

در این مطلب، به آموزش درون یابی در متلب به زبان ساده پرداخته‌ایم. درون یابی به معنای تقریب توابع در یک بازه است. در این‌جا سینتکس دستوری درون یابی در زبان برنامه نویسی متلب را به همراه توضیحات مفصل آن ارائه کرده‌ایم.

Interpolation یا درون یابی در متلب

همان‌طور که در مقدمه‌ی مطلب اشاره کردیم، منظور از درون یابی در متلب، تقریب یک تابع در یک بازه است. فرض کنید یک تابع داریم که ضابطه‌ی آن معلوم نیست و تنها چند نقطه از این تابع روی دستگاه مختصات تعیین شده باشد. درون یابی کمک می‌کند تا نزدیک‌ترین چند جمله‌ای به ضابطه‌ی این تابع را محاسبه کنیم.

بگذارید از منظر دیگری، درون یابی را شرح دهیم. فرض کنید چند نقطه در صفحه‌ی مختصات داریم. می‌خواهیم بفهمیم که کدام منحنی از این نقاط می‌گذرد. به این کار، برازش منحنی می‌گویند. در حقیقت برازش منحنی یک نوع درونیابی با استفاده از نمودار منحنی است.

با توجه به کاربردهای فراوان نرم افزار متلب در محاسبات ریاضی، می‌توان درون یابی را با استفاده از این نرم افزار و زبان برنامه‌نویسی محاسبه کرد. در ادامه، با چگونگی انجام محاسبات درونیابی در متلب آشنا خواهید شد.

سینتکس دستوری در متلب

در این بخش از آموزش درون یابی در متلب، قصد داریم تا چگونگی استفاده از تابع interpn برای درون یابی در زبان متلب، را شرح دهیم. همان‌طور که دیده می‌شود نام این تابع یعنی interpn برگرفته از اختصار اصطلاح درون‌یابی یعنی Interpolation است.

سینتکس دستوری interpn در متلب به یکی از شش صورت زیر است:

Vq = interpn(X1,X2,…,Xn,V,Xq1,Xq2,…,Xqn)

Vq = interpn(V,Xq1,Xq2,…,Xqn)

Vq = interpn(V)

Vq = interpn(V,k)

Vq = interpn(___,method)

Vq = interpn(___,method,extrapval)

در ادامه، هر یک از این دستورات را توضیح داده و با ذکر مثال، مفهوم و کاربرد درونیابی در متلب را بیان کرده‌ایم.

– دستور Vq = interpn(X1,X2,…,Xn,V,Xq1,Xq2,…,Xqn)

فرض می‌کنیم n متغیر داریم. مختصات نقاط نمونه این n متغیر، X1، X2، …، Xn خواهد بود. در واقع X1، X2، …، Xn همان نقاطی هستند که مختصات آن‌ها را داریم و می‌خواهیم به منحنی تابع برسیم. V مقادیر تابع مربوطه (که ضابطه‌ی آن را نداریم) در هر نقطه نمونه است. یعنی مقادیری که اگر X1، X2، …، Xn را در ضابطه‌ی تابع قرار دهیم، به‌آن می‌رسیم. هم‌چنین Xq1، Xq2، …، Xqn مختصات نقاط پرس و جو خواهد بود. (در ادامه‌ی مطلب، شرح مفصل‌تری از این آرگومان‌ها خواهید خواند.) دستور فوق، مقادیر درون یابی تابعی از n متغیر را در نقاط پرس‌وجوی خاص با استفاده از درون یابی خطی برمی‌گرداند.

دستور Vq = interpn(V,Xq1,Xq2,…,Xqn)

این سینتکس، زمانی کاربرد دارد که قصد داریم حافظه‌ را نگه داشته و فواصل بین نقاط برایمان بی‌اهمیت باشد. در این دستور، یک شبکه‌ی پیش فرض از نقاط نمونه ایجاد خواهد شد.

دستور Vq = interpn(V)

در این‌جا، مقادیر درون یابی شده از تابع بر روی یک شبکه تصفیه شده برگردانده خواهد شد. در این‌جا فواصل مقادیر نمونه اهمیت دارد و با تقسیم فاصله بین مقادیر نمونه در هر بعد، شبکه‌ی تصفیه شده ایجاد می‌گردد.

دستور Vq = interpn(V,k)

در این دستور، مقادیر درون یابی شده در یک شبکه‌ی تصفیه شده برگشت داده می‌شود. در این‌جا فواصل بین مقادیر نمونه به تعداد kبار نصف می‌شود. با این روش، تعداد ۲^k-1 نقطه درونیابی بین مقادیر نمونه ایجاد می‌شود.

دستور Vq = interpn(___,method)

این دستور یک روش درونیابی جایگزین را مشخص می‌کند. مثلاً روش خطی، نزدیک‌ترین، pchip، مکعبی، makima و یا spline. در صورتی که متد معین نشود، به‌طور پیش فرض روش خطی در نظر گرفته خواهد شد.

دستور Vq = interpn(___,method,extrapval)

در این دستور نیز یک مقدار اسکالر به تمام پرس‌وجوهای خارج از دامنه‌ی نقاط نمونه، اختصاص داده خواهد شد. اگر آرگومان extrapval را از دستور فوق حذف کنید، یکی از حالات زیر رخ خواهد داد:

• به‌صورت خودکار مقدار برونیابی شده برای یکی از روش‌های spline و یا makima برگشت داده می‌شود.
• مقادیر NaN برای سایر متدهای درون‌یابی در نظر گرفته می‌شود.

درون یابی یک بعدی

منظور از درون یابی یک بعدی، تابعی است که به‌صورت خطی ترسیم می‌شود. در این شکل از درون یابی، چون البع فرم خطی دارد، بین هر دو نقطه، یک خط راست ترسیم خواهد شد.

ابتدا می‌بایست نقاط نمونه و مقادیر آن‌ها در تابع مورد نظر را تعریف کنید. به‌عنوان مثال:

x=[1 2 3 4 5]

v=[12 16 31 10 6]

اکنون می‌بایست نقاط پرس و جو، xq و دستور interpn را تعریف کنیم.

xq=(1:0.1:5)

vq=interpn(x,v,xq,’cubic’);‎

نکته: در این‌جا از سینتکس دستوری اول استفاده شده است. X، v و Vq آرگومان‌های ورودی این سینتکس دستوری هستند. آن‌چه در مقابل xq نوشته شده است، بردار است. این مفهوم در پایان مطلب شرح داده شده است.

برای ترسیم نتیجه (ترسیم منحنی درون یابی شده) می‌نویسیم:

Figure

plot(x,v,’o’,xq,vq,’-‘);‎

legend(‘samples’,’Cubic Interpolation’);‎

توضیحات:

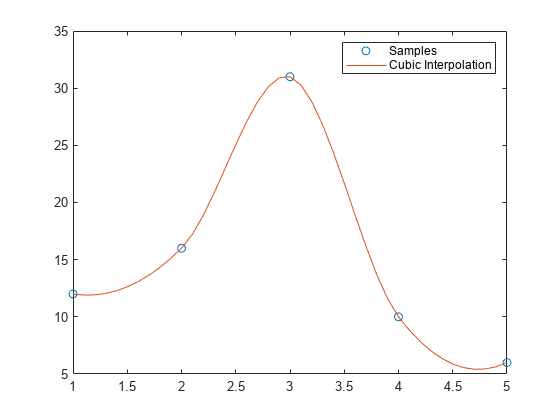
در دستور بالا نقاط نمونه را با عنوان samples مشخص کرده‌ایم و علامت o را به آن اختصاص داده‌ایم. یعنی نقاط (۱,۱۲)، (۲,۱۶)، (۳,۳۱)، (۴,۱۰) و (۵,۶) بر روی صفحه مختصات با علامت o مشخص می‌شوند. حال برحسب xq و vq منحنی درون‌یابی و ترسیم خواهد شد.

درون یابی دو بعدی

نمودار دوبعدی دیگر یک خط راست نیست، این نمودار می‌تواند حالت منحنی داشته باشد. چون در این‌جا دو بعد داریم، می‌بایست مقادیر مانند تار و پود به شکل جدول ارائه شوند. برای استفاده از درون یابی دوبعدی ابتدا می‌بایست مجموعه‌ای از نقاط شبکه و نقاط نمونه ایجاد کنید. می‌نویسیم:

[X1,X2] = ndgrid((-5:1:5));‎

R = sqrt(X1.^2 + X2.^2)+ eps;‎

V = sin(R)./(R);‎

اکنون مقدار ntimes را برابر با یک قرار می‌دهیم و درون‌یابی را در یک شبکه‌ی ظریف‌تر محدود می‌کنیم.

Vq = interpn(V,’cubic’);‎

mesh(Vq);‎

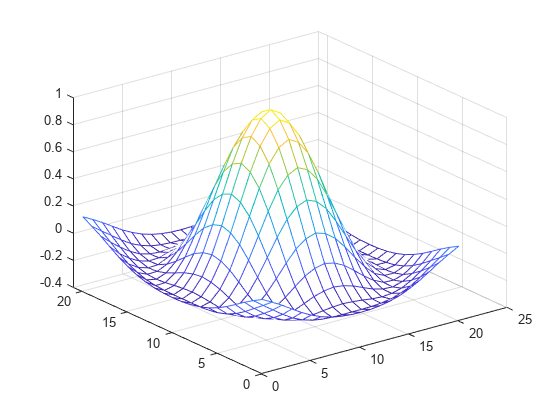
نکته: همان‌طور که اشاره کردیم، در توابع دو بعدی، می‌بایست مقادیر مانند تار و پود به صورت یک جدول ارائه شوند. در این‌ مثال از تابه mesh استفاده شده است.این کار برای حالت‌های بیش‌تر از سه بعد، با تابع ndgrid انجام می‌شود.

درون یابی دو مجموعه از مقادیر نمونه دو بعدی

با استفاده از ndgrid یک شبکه از نقاط نمونه‌ی دوبعدی ایجاد می‌کنیم. برای این منظور، می‌نویسیم:

[x,y] = ndgrid(0:10,0:5);‎

اکنون دو مجموعه مختلف از مقادیر نمونه را در نقاط نمونه ایجاد می‌کنیم. این مقادیر را به‌عنوان صفحه در یک آرایه‌ی سه بعدی به هم متصل کرده و دو مجموعه از مقادیر نمونه در برابر نقاط نمونه را ترسیم می‌کنیم.

v1 = sin(x.*y)./(x+1);‎

v2 = x.*erf(y);‎

V = cat(3,v1,v2);‎

tiledlayout(1,2)

nexttile

surf(x’,y’,V(:,:,1)’)

view(2)

nexttile

surf(x’,y’,V(:,:,2)’)

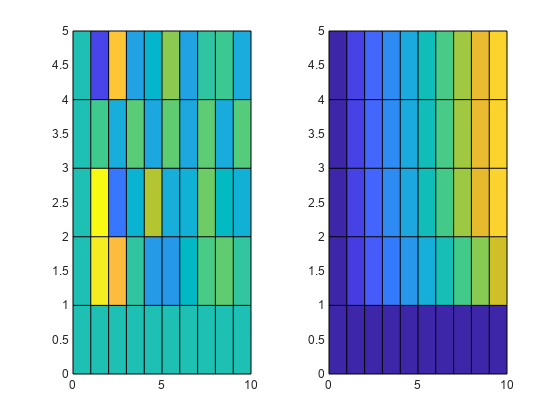
view(2)

چون تابع surf از فرمت meshgrid برای شبکه استفاده می‌کند، می‌بایست ورودی‌ها را برای رسم جابه‌جا کنیم.

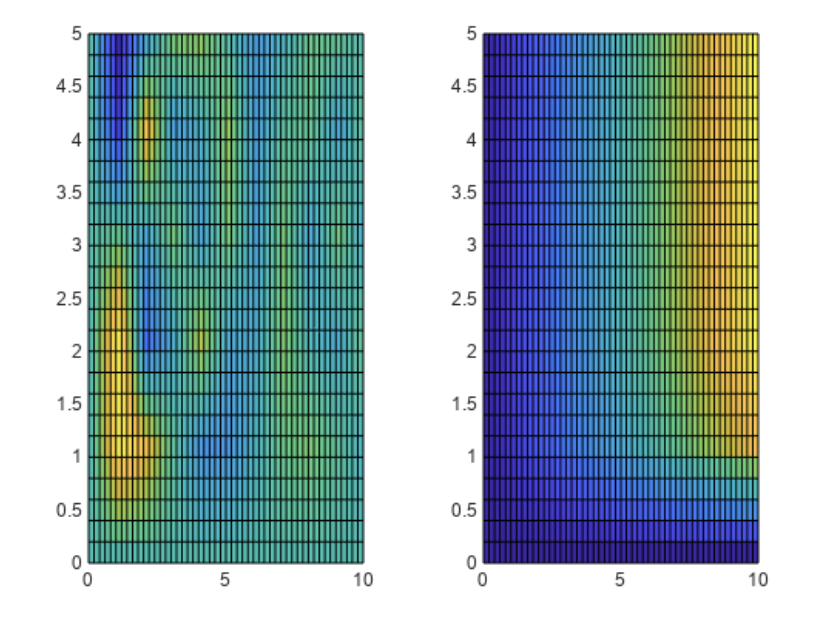
اکنون مجموعه‌ای از نقاط پرس‌وجو برای درونیابی ایجاد می‌کنیم. برای این منظور از تابع ndgrid استفاده می‌کنیم. سپس از interpn استفاده کرده تا مقادبر هر تابع در نقاط پرس‌وجو یافت شود. مقادیر درونیابی شده در برابر نقاط پرس‌وجو ترسیم خواهد شد.

[xq,yq] = ndgrid(0:0.2:10);‎

Vq = interpn(x,y,V,xq,yq);‎

tiledlayout(1,2)

nexttile

surf(xq’,yq’,Vq(:,:,1)’)

view(2)

nexttile

surf(xq’,yq’,Vq(:,:,2)’)

view(2)

ارزیابی دامنه خارج از عملکرد سه بعدی

ابتدا بایست بردارهای شبکه x1، x2 و x3 را ایجاد کنیم. این بردارها، نقاط مرتبط با مقادیر در v را تعریف خواهند کرد.

x1 = 1:100;‎

x2 = 1:50;‎

x3 = 1:30;‎

حال نوبت به تعریف مقادیر نمونه می‌رسد. برای این کار از یک آرایه‌ی ۱۰۰ در ۵۰ در ۳۰ استفاده می‌کنیم. در این آرایه، اعداد تصادفی قرار می‌گیرند.

rng default

V = rand(100,50,30);‎

در مرحله‌ی بعد، v را در سه نقطه خارج از دامنه x1، x2 و x3 ارزیابی می‌کنیم. مقدار extrapval=-1 را تعیین می‌کنیم.

xq1 = [0 0 0];‎

xq2 = [0 0 51];‎

xq3 = [0 101 102];‎

vq = interpn(x1,x2,x3,V,xq1,xq2,xq3,‘linear’,-1)

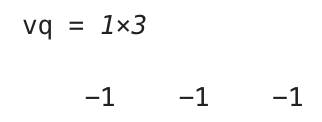
همان‌طور که در تصویر بالا پیداست، هر سه نقطه به -۱ ارزیابی می‌شوند. زیرا خارج از دامنه‌ی x1، x2 و x3 هستند.

درون یابی چهار بعدی در متلب

برای شروع یک تابع با ضابطه‌ی ناشناس که آن را نشان می‌دهد، به صورت زیر تعریف می‌کنیم.

f = @(x,y,z,t) t.*exp(-x.^2 – y.^2 – z.^2);‎

شبکه‌ای از نقاط را در R^4 ایجاد می‌کنیم. سپس تابع را از نقاط عبور می‌دهیم تا مقادیر نمونه v ایجاد شوند.

[x,y,z,t] = ndgrid(-1:0.2:1,-1:0.2:1,-1:0.2:1,0:2:10);‎

V = f(x,y,z,t);‎

اکنون شبکه پرس‌وجو را ایجاد می‌کنیم.

[xq,yq,zq,tq] = …‎

ndgrid(-1:0.05:1,-1:0.08:1,-1:0.05:1,0:0.5:10);‎

حال v را در نقاط پرس‌وجو درون‌یابی می‌کنیم.

Vq = interpn(x,y,z,t,V,xq,yq,zq,tq);‎

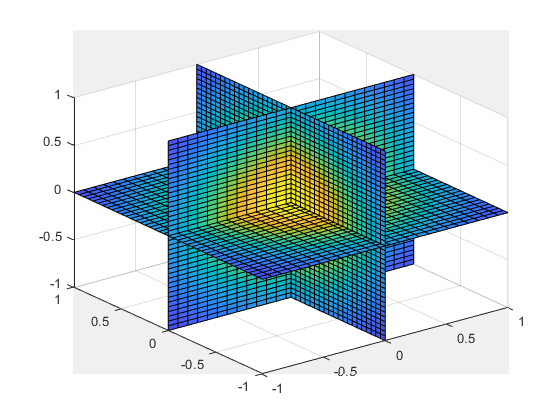
یک فیلم برای نمایش نتایج به‌دست آمده، می‌سازیم.

figure(‘renderer’,’zbuffer’);‎

nframes = size(tq, 4);‎

for j = 1:nframes

slice(yq(:,:,:,j),xq(:,:,:,j),zq(:,:,:,j),…‎

Vq(:,:,:,j),0,0,0);‎

clim([0 10]);‎

M(j) = getframe;‎

end

movie(M);‎

آرگومان‌های ورودی

در آموزش درون یابی در متلب پارامترها و آرگومان‌های ورودی زیادی استفاده شده است. در این بخش، به شرح مفصل این پارامترها پرداخته‌ایم.

به‌طور کلی، شش نوع آرگومان ورودی استفاده شده است.

X1,x2, …, xn- نقاط شبکه نمونه

نقاط شبکه نمونه می‌توانند به‌صورت آرایه یا بردار تعریف شوند. آن‌چه اهمیت دارد این است که نقاط شبکه می‌بایست منحصر به فرد باشند.

در صورتی که نقاط X1,x2, …, xn به‌عنوان آرایه انتخاب شوند، مختصات یک شبکه‌ی کامل (ndgrid) را در بر خواهند گرفت. از تابع ndgrid برای ایجاد آرایه‌های X1,x2, …, xn می‌بایست استفاده شود. ضمناً توجه داشته باشید که اندازه‌های آرایه‌ها باید با هم برابر باشند.

چنان‌چه نقاط X1,x2, …, xn بردار باشند، آن را به‌عنوان بردار شبکه در نظر می‌گیریم. توجه داشته باشید که در این حالت نیز مقادیر این بردارها باید کاملاً یکنواخت باشد. چه بردارها به‌صورت افزایشی باشند و چه در حال کاهش.

مثال:

[X1,X2,X3,X4] = ndgrid(1:30,-10:10,1:5,10:13(‎

*انواع داده در نقاط شبکه نمونه می‌تواند به صورت single و یا double تعریف شود.

V- مقادیر نمونه

مقادیر نمونه به‌صورت یک آرایه تعریف خواهند شد. اندازه‌ی این آرایه بستگی به اندازه‌ی شبکه‌ی نقاط نمونه دارد که توسط X1,x2, …, xn مشخص کرده‌ایم.

همان‌طور که پیش‌تر شرح دادیم، نقاط نمونه X1,x2, …, xn می‌توانند به‌صورت آرایه و یا بردار شبکه باشند. در هر دو صورت یک شبکه‌ی n بعدی خواهیم داشت. متغیر v یک آرایه‌ است که باید حداقل به اندازه‌ی n باشد. البته ابعاد آرایه‌ی v می‌تواند از n نیز بزرگ‌تر باشد.

در صورتی که آرایه‌ی v هم n بعد داشته باشد، انتظار می‌رود تا اندازه‌ی v نیز با اندازه‌ی شبکه‌ی n بعدی که توسط X1,x2, …, xn تعریف شده است، برابر باشد. در این حالت، v مجموعه‌ای از مقادیر نمونه در نقاط نمونه خواهد بود. به عنوان مثال اگر X1,x2, …, xn آرایه‌هایی با ابعاد ۳ در ۳ در ۳ باشند. V نیز می‌توند یک آرایه‌ی با اندازه‌ی ۳ در ۳ در ۳ باشد.

در حالت دیگر، چنان‌چه v بیش‌تر از n بعد داشته باشد، انتظار می‌رود تا n بعد اول v با اندازه‌ی شبکه‌ی n بعدی که توسط X1,x2, …, xn تعریف شده است، مطابقت کامل داشته باشد. ابعاد اضافی v مجموعه‌های اضافی‌تری از مقادیر نمونه در نقاط نمونه را تعریف خواهد کرد.

به عنوان مثال، اگر X1,x2, …, xn آرایه‌هایی با اندازه‌ی ۳ در ۳ در ۳ باشند، v می‌تواند یک آرایه با ابعاد ۳ در ۳ در ۳ در ۲ باشد. در این حالت، دو مجموعه از مقادیر نمونه تعریف می‌شود. در صورتی که v شامل اعداد مختلط باشد، آن‌ها دستور interpn قسمت‌های واقعی و تخمینی را به‌صورت جدا از هم درون‌یابی خواهد کرد. انواع داده می‌تواند به صورت single و یا double تعریف شود. هم‌چنین از نوع داده‌ی پیچیده، پشتیبانی می‌شود.

Xq1,xq2,… , xqn نقاط پرس‌وجو

نقاط پرس‌وجو می‌توانند به‌عنوان اسکالر حقیقی، بردار و یا آرایه تعریف شوند.

• در صورتی که Xq1,xq2,… , xqn اسکالر باشد، آن‌گاه این پارامترها در واقع مختصات یک نقطه پرس‌وجو در R^n خواهند بود.
• در صورتی که Xq1,xq2,… , xqn بردارهایی با جهت‌های مختلف باشند، این پارامترها به‌عنوان بردارهای شبکه‌ی R^n در نظر گرفته می‌شوند. هم‌چنین در صورتی که Xq1,xq2,… , xqn بردارهایی با اندازه و جهت یکسان باشند، این پارامتر به‌عنوان نقاط پراکنده در R^n خواهند بود.
• در صورتی که Xq1,xq2,… , xqn آرایه‌هایی با اندازه‌ی یکسان باشد، آن‌گاه این پارامتر، یک شبکه‌ی کامل از نقاط پرس‌وجو (ndgrid) را نشان می‌دهد.

مثال:

[X1,X2,X3,X4] = ndgrid(1:10,1:5,7:9,10:11)

انواع داده می‌تواند به صورت single و یا double تعریف شود.

K – ضریب پالایش

ضریب پالایش می‌تواند یک متغیر از نوع اسکالر حقیقی و غیر منفی باشد. این ضریب در واقع تعداد دفعاتی که برای تقسیم مکرر فواصل شبکه در هر بعد استفاده می‌شود را تعیین می‌کند. این کار سبب می‌شود تا ۲^k-1 نقطه درون‌یابی بین مقادیر نمونه ایجاد شود.

ناگفته نماند که در صورت که مقدار k برابر با ۰ در نظر گرفته شود، آن‌گاه Vq همان V خواهد بود. هم‌چنین توجه کنید که interpn(V,1) با interpn(V) برابر است. تصویر زیر، k=2 را در R2 نشان می‌دهد. ۷۲ مقدار درون‌یابی به رنگ قرمز و ۹ مقدار نمونه که به رنگ مشکی مشخص شده است.

مثال:

interpn(V,2)

*انواع داده می‌تواند به صورت single و یا double تعریف شود.

متدهای درون یابیدر متلب

متدهای مختلفی در آموزش درون‌یابی در متلب استفاده می‌شود که در جدول زیر در ادامه‌ی مطلب، شرح داده شده‌اند.

نام متد	شرح متد	تداوم متد	توضیحات تکمیلی
Linear	این متد درون‌یابی پیش فرض است. (یعنی اگر نوع متد مشخص نشود، متلب متد linear را در نظر می‌گیرد.) در این متد، مقدار درون‌یابی شده در یک نقطه‌ی پرس‌وجو بر اساس درونیابی خطی مقادیر نقاط شبکه مجاور در هر بعد محاسبه می‌شود.	C^0	این متد، حداقل دو نقطه شبکه در هر بعد نیاز دارد. این متد نسبت به nearest حافظه‌ی بیش‌تری را لازم دارد.
Nearest	در این متد، مقدار دورن‌یابی شده در یک نقطه‌ی پرس‌وجو، مقدار نزدیک‌ترین نقطه شبکه نمونه خواهد بود.	ناپیوسته	به دو نقطه شبکه در هر بعد نیاز دارد. سریع‌ترین محاسبات با حافظه‌ی متوسط را انجام می‌دهد.
Pchip	این متد، درون‌یابی را به شکل مکعبی تکه‌ای انجام می‌دهد با حفظ شکل مقادیر (فقط برای D-1) در نقاط شبکه همسایه.	C^1	حداقل به جهار نقطه نیاز دارد. نسبت به متد linear حافظه و زمان بیش‌تری برای انجام محاسبات می‌برد.
Cubic	در این متد مقدار دورنیابی شده در یک نقطه‌ی پرس‌وجو براساس درون‌یابی مکعبی مقادیر در نقاط شبکه مجاور در هر بعد محاسبه خواهد شد. به عبارت بهتر، درون‌یابی براساس یک پیچش مکعبی است.	C^1	شبکه باید در هر بعد فاصله‌های یکنواخت داشته باشد. اما یکسان بودن نسبت این فواصل در همه ابعاد ضرورتی ندارد. حداقل به چهار نقطه در هر بعد نیاز است. به حافظه و زمان محاسباتی بیش‌تری نسبت به متد linear نیاز است.
Makima	در این متد درون‌یابی در یک نقطه‌ی پرس‌وجو براساس یک تابع تکه‌ای از چند جمله‌ای‌ها با درجه‌ی حداکثری ۳ انجام می‌شود. فرمول akima برای جلوگیری از overshoot اصلاح شده است.	C^1	به حداقل ۲ نقطه در هر بعد نیاز دارد. موج‌های کم‌تری به نسبت متد spline تولید می‌کند. زمان محاسباتی معمولاً در این متد به‌نسبت متد spline کم‌تر است. اما هر دو حافظه‌ی مشابهی را نیاز دارند.
Spline	مقدار درون‌یابی شده در یک نقطه پرس‌وجو در این متد براساس درون‌یابی مکعبی مقادبر در نقاط شبکه مجاور در هر بعد خواهد بود. درون‌یابی براساس یک اسپلاین مکعبی با استفاده از شرایط انتهایی بدون گره است.	C^2	به چهار نقطه در هر بعد نیاز است. به حافظه و زمان محاسباتی بیش‌تری به نسبت متد cubic نیاز دارد.

Extrapval- مقدار تابع خارج از دامنه X1,x2, …, xn

مقدار تابع خارج از دامنه X1,x2, …, xn به‌عنوان یک اسکالر حقیقی و یا پیچیده است. Interpn یا درون‌یابی این مقدار ثابت را برای تمام نقاط خارج از دامنه X1,x2, …, xn برمی‌گرداند. انواع داده می‌تواند به صورت single و یا double تعریف شود. هم‌چنین از نوع داده‌ی پیچیده، پشتیبانی می‌شود.

آرگومان‌های خروجی

در دستورات ذکر شده در متن آموزش درون یابی در متلب، هم‌چنین یک آرگومان خروجی مورد نظر است که در ادامه، شرح داده‌ایم.

Vq- مقادیر درون‌یابی شده

مقادیر درون یابی شده به صورت متغیرهایی از جنس اسکالر، بردار، آرایه‌های حقیقی و یا پیچیده، بازگردانده می‌شود. اندازه و شکل Vq به اندازه‌ و مقدار آرگومان‌های ورودی و سینتکس دستوری که استفاده می‌شود، بستگی خواهد داشت.

• در صورتی که نقاط نمونه با X1,x2, …, xn مشخص شوند و یا از شبکه‌ی پیش فرض استفاده شود و v به اندازه شبکه n بعدی نقاط نمونه باشد، Vq شامل مجموعه‌ای از مقادیر درون‌یابی شده از نقاط پرس‌وجو تعریف شده توسط Xq1,xq2,… , xqn خواهد بود.
  • اگر Xq1,xq2,… , xqn اسکالر باشند، Vq نیز اسکالر خواهد بود.
  • اگر Xq1,xq2,… , xqn بردارهایی با اندازه و جهت یکسان باشند، Vq بردار با اندازه و جهت یکسان خواهد بود.
  • اگر Xq1,xq2,… , xqn بردارهای شبکه‌ای با جهت‌گیری مختلط باشند، Vq آرایه‌ای با اندازه شبکه است که به‌طور ضمنی توسط بردارهای شبکه تعریف شده است.
  • اگر Xq1,xq2,… , xqn آرایه‌هایی با اندازه‌ی یکسان باشند، Vq نیز آرایه‌ای با همان اندازه خواهد بود.
• اگر نقاط نمونه را با X1,x2, …, xn مشخص کنید و یا از شبکه پیش فرض استفاده کنید و v ابعاد بیش‌تری نسبت به شبکه nبعدی نقاط نمونه داشته باشد، Vq شامل مجموعه‌های متعددی از مقادیر درون‌یابی شده در نقاط پرس‌وجو تعریف شده توسط Xq1,xq2,… , xqn خواهد بود. در این مورد، n بعد اول Vq از قوانین اندازه برای یک مجموعه‌ی واحد از مقادیر درون‌یابی شده پیروی می‌کند. اما Vq نیز همان ابعاد اضافی V را با اندازه‌های یکسان دارد.
• با سینتکس‌های interpn(V) و هم‌چنین interpn(V,k)، درون‌یابی شبکه پیش فرض kبار انجام می‌شود. (در صورتی که k=1 باشد، سینتکس به‌صورت interpn(V) خواهد بود). در این وضعیت، Vq آرایه‌ای است با تعداد و ابعاد V که اندازه‌ی بعد آن برابر با ۲^k*(size(V,i)-1)+1 خواهد بود.

شرح اصطلاحات در آموزش درون یابی در متلب

در این بخش از آموزش درون یابی در متلب، برخی از اصطلاحات رایج در آموزش درون‌یابی در متلب را شرح داده‌ایم.

کاملاً یکنواخت

در متن آموزش، بارها و بارها واژه‌ی یکنواخت را به‌کار بردیم. منظور از مقادیر یکنواخت، مجموعه مقادیری است که به‌طور منظم در حال افزایش و یا کاهش باشند.

به عنوان مثال دنباله‌ی اعداد a=[2 4 6 8] یک دنباله‌ی یکنواخت و افزایشی است. این در حالی است که دنباله‌ی b=[2 4 4 6 8] کاملاً یکنواخت نیست زیرا در مقادیر b(2) و b(3) تغییری (افزایش) لحاظ نشده است. دنباله‌ی c=[2 4 6 8 6] یک معکوس بین c(4) و c(5) دارد و به‌همین دلیل به‌هیچ وجه نمی‌توان آن را یکنواخت محسوب کرد.

گرید کامل در قالب ndgrid

برای درون‌یابی، شبکه کامل شامل n آرایه، مقادیر X1,x2, …, xn است که عناصر آن شبکه‌ای از نقاط را در R^n نشان می‌دهد. آرایه‌ی Xi حاوی مقادیر کاملاً یکنواخت و افزایشی است که در بعد I تغییر می‌کند.

از تابع ndgrid برای ایجاد یک شبکه کامل می‌توان استفاده کرد و آن را به interpn منتقل نمود. به عنوان مثال کد زیر یک شبکه‌ی کامل در R^2 با -۱ ≤ X1 ≤ ۳, ۱≤ X2 ≤ ۴ ایجاد می‌کند.

[X1,X2] = ndgrid(-1:3,1:4)‎

بردارهای شبکه

برای درون‌یابی، بردارهای شبکه از n بردار با جهت‌گیری مختلف تشکیل می‌شوند که نقاط یک شبکه را در R^n تعریف خواهند کرد. به‌عنوان مثال، کد زیر بردارهای شبکه را در R^3 و منطقه‌های ۱ ≤ x1 ≤ ۳ ، ۴ ≤ x2 ≤ ۵ و ۶ ≤x3≤ ۸ ایجاد می‌کند.

x1 = 1:3;‎

x2 = 4:5;‎

x3 = 6:8;‎

نقاط پراکنده

برای درون‌یابی، نقاط پراکنده شامل n آرایه با بردار و Xq1,xq2,… , xqn است که مجموعه‌ای از نقاط پراکنده در R^n را تعریف می‌کند. آرایه‌ شامل مختصات در بعد i است.

برای مثال، کد زیر نقاط (۱, ۱۹, ۱۰)، (۶, ۴۰, ۱)، (۱۵, ۳۳, ۲۲)، و (۰, ۶۱, ۱۳) را در R^3 مشخص می‌کند.

Xq1 = [1 6; 15 0];‎

Xq2 = [19 40; 33 61];‎

Xq3 = [10 1; 22 13];‎

جمع بندی

در این مطلب به زبان ساده بیان کردیم که منظور از درونیابی در متلب چیست و چطور می‌توان از این روش استفاده کرد. برای فهم راحت‌تر، مثال‌هایی را در هر مورد ذکر کردیم. امیدواریم بتوانید از این مفاهیم استفاده کنید. توجه داشته باشید که اگر مسأله‌ای در خصوص سینتکس دستوری و دیگر مفاهیم آموزش درون یابی در متلب مبهم بود، تا انتهای مطلب شرح داده شده است.

آموزش متلب در مکتب خونه

اگر به یادگیری متلب علاقه‌مند هستید و می‌خواهید با یادگیری این نرم‌افزار، محاسبات ریاضی و رایانه‌ای خود را بسیار سریع‌تر و ساده‌تر انجام دهید، می‌توانید سری به وب‌سایت مکتب خونه بزنید. در دوره‌های آموزش متلب در مکتب خونه از صفر تا صد کار با نرم افزار متلب را فرا خواهید گرفت. آموزش‌ها به زبان ساده و از سطح مقدماتی آغاز می‌شوند. پس اگر هیچ آشنایی و زمینه‌ای در کار با این برنامه ندارید، می‌توانید از دوره‌های آموزش متلب مکتب خونه استفاده کنید.