اعداد اول یک مفهوم اساسی در ریاضیات هستند و جایگاه ویژهای در دنیای نظریه اعداد دارند. در این مقاله، ما به نحوه محاسبه عدد اعداد اول با پایتون در رویکردهای مختلف میپردازیم. شما چه یک فرد مبتدی باشید و چه یک کدنویس باتجربه، درک اعداد اول از دیدگاههای مختلف میتواند دانش شما را از این اعداد صحیح منحصربهفرد عمیقتر کند. در ادامه انواع کد پایتون عدد اول را مورد بررسی قرار میدهیم. برای کسب اطلاعات بیشتر در این رابطه تا پایان این نوشته از دسته آموزش پایتون با ما همراه باشید.
کد پایتون عدد اول
قبل از اینکه وارد بخش کدنویسی شویم، درک اصول اولیه اعداد اول ضروری است. عدد اول یک عدد صحیح مثبت بزرگتر از ۱ بوده که مقسومعلیه دیگری جز ۱ و خودش ندارد. به عنوان مثال، ۲، ۳، ۵ و ۷ اعداد اول هستند. درک این تعریف بسیار مهم است. ابتدا کد پایتون عدد اول را با رویکرد ساده مورد بررسی قرار خواهیم داد که به صورت زیر است:
def is_prime(number):
if number خورجی کد فوق به صورت زیر است:
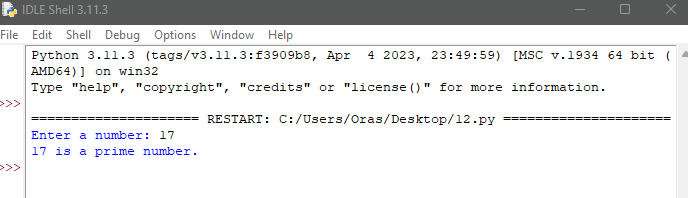
کد فوق عددی از کاربر گرفته و مشخص میکند که آیا این عدد اول است یا خیر.
کد پایتون عدد اول با رویکرد Brute Force
سادهترین راه برای محاسبه اعداد اول با استفاده از روش brute force است. در پایتون، میتوانیم این را با بررسی اینکه آیا یک عدد n بر هر عدد صحیح بین ۲ و جذر n بخشپذیر است یا خیر، پیادهسازی کنیم. اگر مقسومعلیه پیدا نشد، عدد اول است. این رویکرد، اگرچه ساده بوده، اما به دلیل پیچیدگی زمانی، برای اعداد بزرگتر ناکارآمد میشود. در اینجا مثالی از نحوه پیادهسازی روش brute force برای یافتن اعداد اول در پایتون آورده شده است:
def is_prime_brute_force(n):
if n خروجی کد بالا به صورت زیر است:
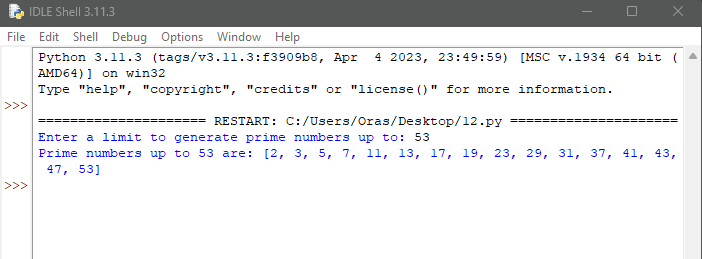
در کد پایتون عدد اول بالا، تابع «is_prime_brute_force» به عنوان نوعی تابع عدد اول در پایتون با آزمایش قابلیت بخشپذیری آن با همه اعداد بین ۲ و «n – 1»، اول بودن یک عدد «n» را بررسی میکند. تابع generate_primes_brute_force فهرستی از اعداد اول را با استفاده از رویکرد brute force تا سقف مشخصی تولید میکند. لطفاً توجه داشته باشید که روش brute force برای اعداد بزرگتر به دلیل پیچیدگی زمانی O(n) کارآمد نیست و آن را برای محاسبه اعداد اول فراتر از یک محدوده خاص غیرعملی میکند.
روش غربال اراتوستن برای محاسبه عدد اول
برای محاسبه مؤثر اعداد اول تا حد معین، غربال اراتوستن روشی مناسب است. این الگوریتم یونان باستان همه اعداد اول را در یک محدوده مشخص شناسایی میکند. میتوانیم این الگوریتم را با استفاده از لیستها در پایتون پیادهسازی کنیم. با علامتگذاری مکرر مضرب هر عدد اول، میتوانیم اعداد غیر اول را غربال کرده و اعداد اول را در محدوده نشان دهیم. در اینجا مثالی از کد پایتون عدد اول با روش Sieve of Eratosthenes برای یافتن اعداد اول آورده شده است:
def sieve_of_eratosthenes(limit):
primes = [True] * (limit + 1)
primes[0] = primes[1] = False
for num in range(2, int(limit ** 0.5) + 1):
if primes[num]:
for multiple in range(num * num, limit + 1, num):
primes[multiple] = False
prime_list = [num for num, is_prime in enumerate(primes) if is_prime]
return prime_list
limit = int(input("Enter a limit to generate prime numbers up to: "))
prime_list = sieve_of_eratosthenes(limit)
print("Prime numbers up to", limit, "are:", prime_list)خروجی کد بالا به صورت زیر است:
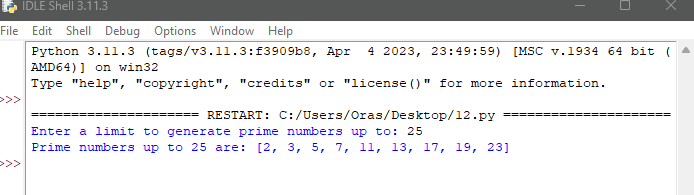
در این مثال، تابع «Seve_of_eratosthenes» از الگوریتم Sieve of Eratosthenes برای تولید فهرستی از اعداد اول تا سقف مشخص شده استفاده میکند. الگوریتم با علامتگذاری مکرر مضرب هر عدد اول که از ۲ شروع میشود، کار میکند و پس از تکمیل فرآیند، اعداد بدون علامت باقی مانده اول هستند. غربال اراتوستن به طور قابل توجهی کارآمدتر از روش brute force است، با پیچیدگی زمانی تقریباً O (n log log n). این آن را برای تولید اعداد اول در محدودههای بزرگتر مناسب میکند.
استفاده از کتابخانههای پایتون برای محسابه عدد اول
پایتون کتابخانههای قدرتمندی مانند SymPy را ارائه میدهد که محاسبات اعداد اول را ساده میکند. SymPy توابعی را برای تولید اعداد اول، بررسی اولیه بودن،و حتی انجام عملیات مربوط به اعداد اول ارائه میدهد. استفاده از کتابخانههای پایتون میتواند در زمان صرفهجویی کرده و راهحلهای بهینهتری را در مقایسه با اجرای الگوریتمها از ابتدا ارائه دهد. در اینجا مثالی از نحوه استفاده از کتابخانه SymPy برای تولید اعداد اول در پایتون آورده شده که کد پایتون عدد اول در این مثال به صورت زیر است:
from sympy import primerange
limit = int(input("Enter a limit to generate prime numbers up to: "))
prime_list = list(primerange(2, limit + 1))
print("Prime numbers up to", limit, "are:", prime_list)خروجی مثال بالا به صورت زیر است:
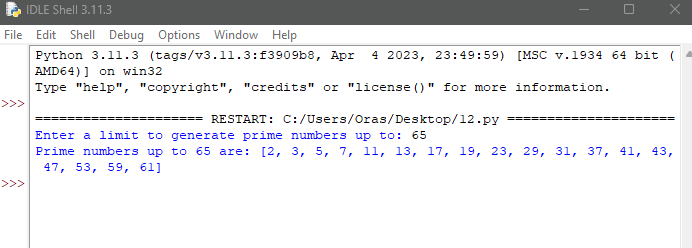
در این مثال، ما از تابع “primerange” از کتابخانه SymPy استفاده میکنیم. تابع “primerange” نوعی پیمایش روی اعداد اول در یک محدوده مشخص انجام میدهد که سپس آن را به یک لیست تبدیل میکنیم.
SymPy یک کتابخانه قدرتمند برای ریاضیات نمادین است، از جمله ویژگیهای مربوط به اعداد اول مانند آزمایش اولیه، تولید اعداد اول و غیره. با استفاده از توابع داخلی SymPy، میتوانید از الگوریتمهای بهینه و محاسبات کارآمد برای اعداد اول و عملیات ریاضی مرتبط بهره ببرید.
قضایای اعداد اول
با نگاهی به اعداد اول از منظر نظری، قضایای اعداد اولرا داریم که بینشهایی را در مورد توزیع اعداد اول ارائه میدهند. به عنوان مثال، قضیه اعداد اول چگالی مجانبی اعداد اول را در بین تمام اعداد صحیح مثبت توصیف میکند. در حالی که این روش به طور مستقیم برای تولید اعداد اول استفاده نمیشود، اما درک این قضایا به دانش ریاضی شما اضافه میکند.
الگوریتمهای پیشرفته عدد اول در پایتون
برای کسانی که به دنبال چالش کدنویسی هستند، تحقیق در انواع الگوریتم اعداد اول پیشرفته مانند آزمون اولیه میلر-رابین یا آزمون اولیه AKS میتواند مفید باشد. این الگوریتمها به سناریوهایی پاسخ میدهند که در آن دقت و قابلیت اطمینان از اهمیت بالایی برخوردار است.
سخن پایانی
در این مطلب آموزشی از مکتوب، روشهای مختلفی را برای محاسبه اعداد اول از دیدگاههای مختلف پوشش دادهایم. فرقی نمیکند رویکرد brute force ساده را انتخاب کنید، کارایی غربال اراتوستن، یا راحتی کتابخانهها، هر روش به درک شما از اعداد اول کمک میکند. علاوه بر این، بررسی قضایای اعداد اول و الگوریتمهای پیشرفته ماهیت عمیق این اعداد صحیح را به شما نشان میدهد.
کد پایتون عدد اول را برای تشخیص اعداد اول میتوانید در انواع زبانهای برنامهنویسی دیگر مانند جاوا، جاوا اسکریپت، سی پلاس پلاس (c++) و غیره نیز بررسی کنید. به امید اینکه تمرین برنامه نویسی پایتون بالا در رابطه با محاسبه عدد اول برای شما مفید واقع شده باشد.








