آموزش حل معادلات در متلب، یکی از پرطرفدارترین موضوعات آموزشی است. حل معادلات ریاضی، گاه بسیار زمانبر و دشوار است. لذا حل این معادلات بهکمک نرم افزار متلب، یک راهکار سریع، ساده و مطمئن است. در این مطلب، چگونگی انجام این کار را شرح دادهایم.
معادلات در ریاضی
معادله، گزارهای است که تساوی بین دو عبارت جبری را نشان میدهد. در طرفین معادله (دو طرف علامت تساوی)، میتوان مجهولاتی نوشت. بهعنوان مثال وقتی مینویسیم: x+2=10 یک معادلهی یک مجهولی ساده نوشتهایم. در این مثال، ۲+x در یک طرف تساوی و ۱۰ در طرف دیگر واقع شده است. x مجهول این معادله محسوب میشود.

معادلات ریاضی انواع مختلفی دارند. معادلات چند جملهای و معادلات چند خطی در جبر، معادلات ضمنی در هندسه، معادلات مثلثاتی، معادلات نمایی، دستگاه معادلات و غیره برخی از رایجترین انواع معادله در ریاضیات هستند.
همانطور که اشاره کردیم، حل معادلات ریاضی همیشه ساده نیست. لذا میتوان از نرم افزارهای محاسباتی در این زمینه کمک گرفت. در این مطلب به آموزش حل معادلات در متلب (برای انواع مختلفی از معادلات ریاضی) پرداختهایم. در متلب کافی است تا از دستورات و توابع مربوط به حل معادله (برحسب نوع آن) استفاده کنیم.
تعریف معادله در متلب
پیش از آنکه به آموزش حل معادلات در متلب بپردازیم، ضروری است تا با شیوهی تعریف معادله در این نرم افزار آشنا شویم.

بهطور کلی میدانید که دو معادلهی x+y=1 و x+y-1=0 با هم یکسان هستند. در این دو معادله، تنها عدد ثابت از یک سمت تساوی، بهسمت دیگر کشیده شده است. به دلیل همین جابهجایی، علامت آن نیز تغییر کرده است. در متلب، شکل دوم این معادلات رایجتر است. البته برای حالت اول میتوان از علامت == استفاده کرد. یعنی:
x+y==1
یا
x+y-1=0
ضمناً شما میتوانید هر معادله را در یک متغیر ذخیره کنید. در این صورت برای حل معادلات با دستورات دیگر، شکل سینتکس سادهتر شده و از سردرگمی شما میکاهد. در ادامهی مطلب با این موضوع بیشتر آشنا خواهید شد.
حل معادله در متلب با دستور solve
یکی از سادهترین انواع معادلات ریاضی، معادلات جبری هستند. در این بخش به آموزش حل معادلات جبری در متلب میپردازیم. این تابع بهصورت زیر نوشته میشود:
solve(متغیر, معادله)که میتوان مقدار نتیجهی این تابع را در یک متغیر دیگر ذخیره کرد. یعنی بنویسیم:
solve = result (متغیر, معادله)همانطور که ملاحظه میشود در سینتکس دستوری این تابع، دو آرگومان ورودی دریافت میشود. اولین آرگومان معادلهای است که میخواهیم با دستور solve حل شود. پارامتر دوم نیز متغیری است که میخواهیم نتیجهی آن برگردانده شود.
بهعنوان نمونه اگر بخواهیم معادلهی x+2=5 را حل کنیم، باید بنویسیم:
result= solve(x+2=5, x)
یا میتوان نوشت:
eq=x+2-5;
result= solve (eq, x)در این دستور، مقدار x برای معادلهی x+2=5 یا x+2-5=0 محاسبه و در متغیر result ذخیره خواهد شد.
نکته: در صورت تعیین نشدن آرگومان دوم، یعنی متغیر مورد نظر، متلب بهطور پیشفرض معادله را برای متغیر x حل میکند. تعیین این آرگومان برای معادلات چند مجهولی، اهمیت دارد.
حل معادله درجه ۲ در متلب با دستور solve
دستور solve همچنین برای حل معادلات درجه ۲ و بالاتر کاربرد دارد. معادلهی درجهی دو، معادلهای خواهد بود که بالاترین توان متغیر در آن ۲ است. فرم کلی معادلهی درجهی ۲ بهصورت ax^2+bx+c=0 نوشته میشود. با این شرط که در آن a برابر با صفر نباشد.
برای حل معادلهی درجه ۲ در متلب، تابع solve نتیجه را در یک آرایه برمیگرداند. برای این منظور مینویسیم:
result= solve(x^2+۷*x+۱۲=۰, x)
در این مثال، عبارت x^2+۷*x+۱۲=۰ یک معادلهی درجه ۲ است. با توجه به سینتکس دستور solve، میخواهیم مقدار متغیر x محاسبه و در متغیر result برگردانده شود.
توجه داشته باشید که جوابهای معادلهی درجه ۲ اغلب دو پاسخ است. زیرا معمولاً معادله بهازای دو مقدار از مجهول x صحیح میشود. برای حل معادله درجه ۲ بهصورت دستی، اغلب از روشهای فاکتورگیری، اتحاد و یا فرمول مخصوص (استفاده از دلتا) استفاده میشود.
در این مثال چون معادله درجه ۲ است، نتیجه برابر است با:
x=3 و x=4
چنانچه ملاحظه میشود، مقدار ۳ و مقدار ۴ در این معادله، آن را با ۰ برابر میکند. در متلب، نتیجه بهصورت زیر قابل دسترس خواهد بود.
result(1)= 3 result(2)= 4
که برای چاپ آن میتوان از دستور disp استفاده کرد. یعنی بنویسیم:
disp(result(1)), disp(‘and’), disp(result(2))که نشان میدهد:
۳ and 4حل معادله درجه ۳ در متلب
طبق تعریفی که برای معادلات درجه ۲ ارائه دادیم، معادلهی درجهی سه، معادلهای خواهد بود که بالاترین توان متغیر در آن برابر با ۳ است. فرم کلی یک معادلهی درجه ۳ بهصورت ax^3+bx^2+cx+d=0 است.
حل معادلات درجه ۳ در متلب نیز به روش ذکر شده در بخش قبل انجام میشود. به عنوان مثال، فرض میکنیم که معادلهی درجه سه زیر را داشته باشیم.
x^3+2x^2+x+4=8
برای حل این معادله در متلب کافی است بنویسیم:
result= solve(x^3+2x^2+x+4=8, x)
نتیجه در آرایهی result برگشت داده خواهد شد. دقیقاً مشابه آنچه در بخش حل معادله درجه ۲ بیان کردیم، میتوان به پاسخها دسترسی داشت.
نکته: در معادلات درجه ۳ و بالاتر از آن، این احتمال وجود دارد که نتایج بهدست آمده، اعدادی با اعشار بزرگ باشند. برای کوچکتر کردن نتیجه، بهتر است از فرمت double استفاده کنید. فرمت double تنها تا چهار رقم پس از اعشار را نشان میدهد.
حل معادله چند پارامتری در متلب
در این بخش از آموزش حل معادلات در متلب، به چگونگی حل معادله چند پارامتری در متلب پرداختهایم. معادلهی پارامتری مجموعهای از معادلات هستند که یک یا چند متغیر بهغیر از x در آن وجود دارد. در مثال قبلی، هریک از معادلات x+2=5 و x^2+۷*x+۱۲=۰ شامل یک متغیر x هستند. اما در معادلات چند پارامتری، علاوه بر x متغیرهای دیگر نیز حضور دارند. x=2y یک معادلهی چند پارامتری است. هم x و هم y در این معادله، متغیر خواهند بود.

معادلات چند پارامتری، به ازای ورودیهای مختلف، مقادیر متفاوتی خواهند داشت. در معادلهی x=2y اگر برای y مقادیر ۱، ۲ و ۳ را قرار دهیم، x بهترتیب مقدار ۲، ۴، ۶ را دریافت میکند. برای حل این چنین معادلاتی در متلب، میتوانیم از تابع vpasolve استفاده کنیم. این تابع امکان تعریف یک بازه را میدهد. مینویسیم:
result= vpasolve(x=2y, y,[1 5])این دستور سبب میشود تا متلب مقادیر x بهازای yهای از ۱ تا ۵ را بیابد. بنابراین داریم:
result(1)=2,result(2)=2,result(3)=6,result(4)=8,result(5)=10
حل دستگاه معادلات در متلب
دستگاه معادلات، از چند معادله تشکیل شده است. حل چند معادله چند مجهول در متلب از طریق حل دستگاه معادلات قابل انجام است. در متلب، برای حل دستگاه معادلات، میتوانیم از دستور solve استفاده کنیم. به این صورت که مینویسیم:
solve([متغیر دوم, متغیر اول],[معادله دوم, معادله اول])
مثلاً فرض میکنیم که دستگاه معادلات خطی، شامل دو معادله بهصورت زیر است:
x+3y=4 4x-3y=1
برای حل این دستگاه در متلب مینویسیم:
[result_x, result_y]=solve([x+3y=4, 4x-3y=1],[x,y])
متلب مقادیر result_x=1 و result_y=1 را برمیگرداند.
حل دستگاه معادلات با تابع roots
روش دیگر برای حل دستگاه معادلات درجه دوم، استفاده از تابع roots است. تابع roots ریشههای چند جملهای را برمیگرداند. این تابع، ضرایب معادله را بهعنوان آرگومان ورودی دریافت میکند.
بهعنوان مثال برای معادلهی x^2-3x+2=0 میتوان نوشت:
Roots ([1 -3 2])
از روی این سینتکس، متلب متوجه میشود که معادلهی درجه ۲ با ضریب ۱ برای x^2، ضریب -۳ برای x و ثابت ۲ است. نتیجه به شکل ۲ و ۱ خواهد بود.
نکته: برای معادلات درجه سوم، امکان استفاده از تابع roots به همین شکل وجود دارد. تنها تفاوت، درج ضریب x^3 در آرگومان ابتدایی تابع است.
حل دستگاه معادلات به روش کرامر در متلب
روش دیگر برای حل دستگاه معادلات در متلب، روش کرامر است. در این بخش به آموزش حل معادلات در متلب بهروش کرامر پرداختهایم.
قاعدهی کرامر برای حل دستگاه معادلات خطی کاربرد دارد. معادلات در این دستگاه میبایست از نظر تعداد مجهولات با هم برابر باشند. در این روش، میبایست ماتریس مربوط به دستگاه ساخته شود. با محاسبهی دترمینان ماتریس، میتوان معادله را بهروش کرامر حل کرد.
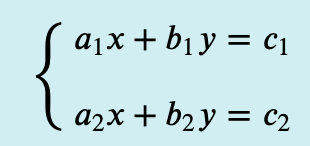
تصور کنید دو معادله در دستگاه معادلات به فرم زیر تعریف شوند.
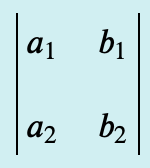
در اینجا میخواهیم ابتدا ماتریس ضرایب معادلات را بسازیم. تصویر زیر، این ماتریس را نشان میدهد.
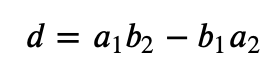
اکنون دترمینان این ماتریس را محاسبه میکنیم. برای محاسبهی دترمینان، از فرمول تصویر زیر استفاده کنید.
اکنون دترمینان برای این دو ماتریس زیر را محاسبه میکنیم. این دو ماتریس از جایگزین کردن مقادیر a و (بار دیگر مقادیر b) با مقادیر c حاصل شده است.
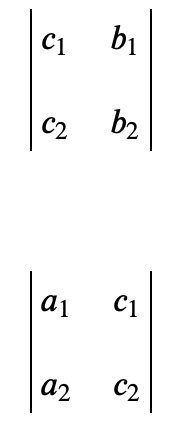
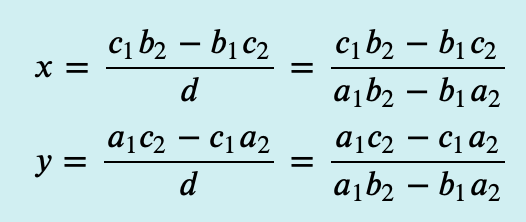
طبق قانون کرامر، اکنون با بهدست آوردن مقادیر دترمینان ماتریسهای فوق، میتوانید از فرمولهای زیر برای بهدست آوردن مقادیر دستگاه فوق استفاده کنید.
توجه داشته باشید که مخرج فرمول مربوط به x و y دترمینان محاسبهشده برای ماتریس اول و صورتهای این فرمول از دترمینان ماتریسهای دوم و سوم بهدست آمده است.
پیادهسازی دترمینان در متلب
برای حل معادله به روش کرامر در نرم افزار متلب، کافی است تا ماتریسی برای ضرایب معادلات و ماتریسی برای ثابتهای معادلات درآوریم. بهعنوان مثال در نظر بگیرید دستگاه معادلات زیر را داریم.
x+3y=4 4x-3y=1
ماتریس ضرایب این دستگاه بهصورت زیر تعریف میشود:
A=[1 3; 4 3]
همچنین برای ثابتهای این دستگاه معادلات، ماتریس زیر را مینویسیم:
B=[4;1]
نتیجهی دستگاه از تقسیم این دو ماتریس بهدست خواهد آمد. بنابراین مینویسیم:
AB یا inv(A)*B
جمعبندی
حل معادله در متلب، بسیار سادهتر، سریعتر و دقیقتر از روشهای محاسبات دستی است. به همین دلیل آموزش حل معادلات در متلب، در شمار پرکاربردترین سرفصلهای آموزشی این نرم افزار است.

در این مطلب، آموزش حل معادلات در متلب را به زبان ساده بیان کردیم. ابتدا معادلات ریاضی را شرح داده و سپس روش حل آن را بهتفکیک نوع معادله بیان کردیم. حل معادلات خطی درجه دو، سه و همچنین حل دستگاه معادلات از روشهای مختلف آموزش داده شد. حل معادله مختلط در متلب با توجه به نکات همین مطلب قابل انجام خواهد بود.
در این آموزش، به منظور سادهسازی مطلب، از مثالهای ساده و مبتدی برای چگونگی استفاده از توابع در متلب استفاده کردیم. شما میتوانید تکنیکهای آموزشی را با مثالهای پیچیدهتر نیز تمرین کنید.
آموزش متلب در مکتب خونه
متلب نرم افزار بسیار قوی و کاربردی برای انجام محاسبات ریاضی است. یادگیری این برنامه بهخصوص به دانشجویان علوم پایه و رشتههای مهندسی، بهشدت توصیه میشود. اگر دوست دارید از صفر تا صد متلب را به زبان ساده یاد بگیرید، میتوانید از دورههای آموزش متلب در مکتب خونه استفاده کنید. در مکتب خونه، آموزش متلب از مبتدی تا سطوح پیشرفتهتر قرار دارد. تمرینهای عملی و ذکر مثالهای فراوان در این دورهها سبب میشوند تا بهخوبی مطالب را فرا بگیرید. امکان کسب مدرک مکتب خونه بعد از گذراندن دورهها نیز وجود دارد.